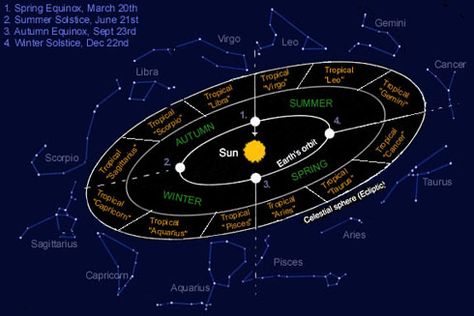
Tropikal Zodyak (Burçlar) Neden Değişmezdir?
Doğuş zamanlarının hesaplanması oldukça eskiye dayanır. Neugebauer’in “Antik Matematiksel Astronomi Tarihi” (A History of Ancient Mathematical Astronomy) eserine göre Babilliler’in “Sistem A” adını verdikleri, doğuş zamanlarının şeması olan bir sistemleri vardı. Doğuş zamanları, o günkü koşullarda bilgisayarlar olmadığı için kolayca modern trigonometrik metotlarla değil sayı dizileriyle hesaplanıyordu. Şöyle ki; Bahar Ekinoksu’yla birlikte zodyağın ilk 30 derecelik segmentine, eğik yükseklik derecesi (Oblique Ascension) sebebiyle, 20 derecelik bir sağ açıklık derecesi (Right Ascension) verilmişti.
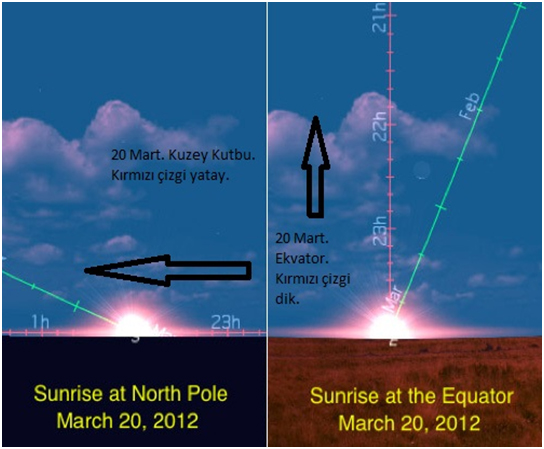
Eğik yükseklik derecesinin ne olduğuna kısaca değinmek gerekirse; Ekvator üzerindeki her noktada Güneş tam sağdan (right) ve dik olarak doğar. (Şekil_1) Ancak kuzeye ya da güneye gidildikçe Güneş, ekvatorda ölçüldüğü gibi tam doğudan ve dik olarak değil de belli bir eğriyi izleyerek göksel ekvatorun başka bir derecesinde doğar. İşte buna eğik yükseklik derecesi (Oblique Ascension) adı verilir. Sistem A’yı yaratanlar muhtemelen Bahar Ekinoksu’nun gerçekleştiği gün bulundukları yerde Güneş’in tam doğudan ve dik olarak doğmadığını fark edip sonrasında 20 derecelik sağ açıklık derecesine ulaştılar.
Bu bilgilerden sonra geri dönersek 20 derecelik sağ açıklık derecesine sahip birinci segmentten altıncı segmente kadar, her 30 derecelik segmente bir öncekinden 4 derece daha fazla sağ açıklık derecesi verilirdi. Altıncı ve yedinci segmentler aynı sağ açıklık derecesine sahiptiler ve yedinciden sonraki her segment, on ikinci yani son segment ilk segmentle aynı dereceye gelene kadar 4 derece azaltılarak devam ediyordu. Altıncı ve yedinci segmentlerin her biri 40 derece sağ açıklık derecesine sahiptiler. Bu 30 derecelik kısımları burçlardan çok segment olarak tanımlıyoruz çünkü Neugebauer’in aktardıklarına göre Bahar Ekinoksu noktasında 30 derecelik ilk segment varsayıldığı gibi 0 derece Koç’tan değil 10 derece Koç’tan başlıyordu. Bu durumda Bahar Ekinoksu noktasının Sidereal şartlara göre hesaplandığı ortada olsa da konuyla ilgili akademisyenler bu fikre pek katılmıyorlar. Bu durumda Babilliler, günışığının eşit olduğu Bahar Ekinoksu noktasını zodyakta sabit bir nokta olarak belirlemiş ve işleyişi buna göre kurmuşlar ya da devam ettirmişlerdir gibi bir sonuç çıkarılabilir.
Eğer Neugebauer’in eserindeki doğuş zamanlarını nominal değer olarak alırsak bu durumda bir şekilde bu sistemi geliştiren Babilliler’in Bahar Ekinoks noktasından itibaren ölçülen 30 derecelik “burçlar” ve 30 derecelik “segmentler” arasındaki farktan haberdar olduklarını bir şekilde onaylamak zorundayız. Yine de konumuz Babilliler’in kaymanın bilincinde olup olmaması değil, tropikal zodyağın neden değişmez ve sürekli sorgulanmasının mantıksız olduğunu anlatmak.
Aşağıdaki tablo Babillilerin Sistem A’da verilen, Bahar Ekinoksu’ndan itibaren 30 derecelik segmentlerin doğuş saatleridir;
|
System A R Sum Su Lg Daylight (h:m) R1 20 20 Ar 10 12:00 R2 24 44 Ta 10 13:20 R3 28 72 Ge 10 14:08 R4 32 104 Cn 10 14:24= Max. R5 36 140 Le 10 14:08 R6 40 180 Vi 10 13:20 R7 40 220 Li 10 12:00 R8 36 256 Sc 10 10:40 R10 28 316 Cp 10 9:36 = Min. R11 24 340 Aq 10 9:52 R12 20 360 Pi 10 10:40
|
Tablo Neugebauer’in eserinden baz alınarak oluşturulmuştur.
Soldan sağa;
- kolon (R1, R2, vs.) : 12 segmenti;
- kolon (R); sağ açıklık derecelerini;
- kolon (Sum): Ekinoks noktasından itibaren toplam dereceleri;
- kolon (Su Lg); kuvvetle muhtemel Sidereal olarak ölçülmüş ve Bahar Ekinoksu
- noktasını 10 derece Koç’tan başlatan- her 30 derecelik segmenti ;
- kolon da (Daylight): Güneş belirtilen noktada olduğu zaman ki gündüz saatlerini
- gösteriyor.
Güneş bahar ve sonbahar ekinoks noktalarındayken gündüz saatlerinin 12 saat, yaz gündönümü noktasındayken 14 saat 24 dakika ve kış gündönümü noktasındayken 9 saat 36 dakika olduğunu fark etmişsinizdir. Ayrıca en uzun gündüzün en kısa gündüze oranının tam olarak 3’e 2 olduğuna da dikkat ediniz. Antik çağlarda enlem bu orana göre ölçülüyormuş.
Başka bir Babil ekolünün geliştirdiği Sistem B olarak adlandırılan ikinci bir sistem daha vardır. Bu sistemde 30 derecelik segmentler, Bahar Ekinoks noktası 8 derece Koç baz alınarak bölümlenmiştir. Çok açık bir şekilde görülüyor ki bu sistem sonradan geliştirildiği ve arada Sistem A ile arasında 2 derecelik fark olduğu için Bahar Ekinoks noktası Sidereal Zodyak’a göre ölçülmüştür. Bu durum yine Babillilerin Hiparkos’tan önce durumun farkında olduklarını doğrular nitelikte. Aşağıdaki tabloda Sistem B’nin doğuş zamanları var.
Değerler Sistem A’dan biraz farklı olsa da geliştirilme mantığı aynı:
|
R Sum SU LG Daylight (h:m) R1 21 21 Ar 8 12:00 R2 24 45 Ta 8 13:12 R3 27 72 Ge 8 14:00 R4 33 105 Cn 8 14:24 = Max. R5 36 141 Le 8 14:00 R6 39 180 Vi 8 13:12 R7 39 219 Li 8 12:00 R8 36 255 Sc 8 10:48 R9 33 288 Sg 8 10:00 R10 27 315 Cp 8 9:36 = Min. R11 24 339 Aq 8 10:00 R12 21 360 Pi 8 10:48
|
Sistem B’yi eserde aktarılanların yarım kalmaması için ekliyoruz. Bahar Ekinoks noktasının 8 derece Koç olması dışında dikkat edeceğimiz başka bir şey olmayacak. Sistem A üzerinden konuşacağız.
İki tabloda da karşıt olan 30 derecelik segmentlerin (R1-R7, R2-R8, R3-R9, R4-R10, R5-R11, R6-R12) toplamının 60 derece olduğunu, ayrıca ilk ve son segmentlerin aynı sağ açıklık derecelerine (R) sahip olduğunu fark ettiniz değil mi? Ya da ikinci segment ile on birinci segmentin, ya da üçüncü ile onuncu segmentin? Bu simetri daha sonra göstereceğimiz nedenler için önemli.
Aşağıda tropik segmentlerin günümüz değerleri kullanılarak hesaplanmış doğuş zamanlarının manuel Sistem A değerleri ile karşılaştırmasını yapalım:
(20 00 ya da 20 18 vb. aralarındaki boşlukları 20 derece 00 dakika ya da 20 derece 18 dakika vs. olduğuna dikkat ediniz.)
|
Segments R1-R12 R2-R11 R3-R10 R4-R9 R5-R8 R6-R7 System A 20 00 24 00 28 00 32 00 36 00 40 00 501 B.C.E. 20 18 23 42 29 40 34 49 36 07 35 24 |
Tablonun son satırında M.Ö 501 yılı için modern trigonometrik metotlarla hesaplanmış sağ açıklık derecelerini görüyoruz. R1-R12, R2-R11 ve R5-R8 segmentlerinde örtüşme aynı. Diğerlerinin arasında ise çok açık farklar yok. Ayrıca bu 30 derecelik segmentler için Bahar Ekinoksu noktasından itibaren hesaplanmış ve tropikal burçlara uyan doğuş zamanlarının zaman içinde gayet sabit kaldığına dikkat çekmek gerek. Aşağıdaki tablo M.Ö 501 ve M.S 2000 yılları için hesaplanmış doğuş zamanlarını gösteriyor. Segment sözcüğünü şimdi burç ile değiştirelim;
Babil’de Tropikal Burçların Doğuş Zamanları:
|
Ar-Pi Ta-Aq Ge-Cp Cn-Sg Le-Sc Vi-Li 501 B.C.E. 20 18 23 42 29 40 34 49 36 07 35 24 2000 C.E. 20 28 23 48 29 40 34 42 36 01 35 21
|
Gördüğünüz gibi farklar oldukça küçük. Yani Tropikal Burçların doğuş zamanları aslında zaman içerisinde aynı kalmış gözüküyor. Karşılaştırma yapmak amaçlı aynı dönemleri içeren, yine modern metotlarla ancak bu sefer Fagan-Allan ayanamsha olarak hesaplanmış
Sidereal burçların doğuş zamanlarına bakalım;
Babil’de Sidereal Burçların Doğuş Zamanları:
|
Ar Ta Ge Cn Le Vi 501 B.C.E. 21 04 25 30 31 42 35 40 35 55 35 15 Pi Aq Cp Sg Sc Li 501 B.C.E. 19 56 22 12 27 33 33 29 36 04 35 39 Ar Ta Ge Cn Le Vi 2000 C.E. 20 13 20 49 24 42 30 44 35 12 35 57 Pi Aq Cp Sg Sc Li 2000 C.E. 22 59 28 34 34 04 36 01 35 28 35 16
|
Tabloyu incelediğimizde iki şey gözümüze çarpıyor. Birincisi Sidereal burçların doğuş saatleri sabitlik göstermiyor. Dikkat ederseniz özellikle Sidereal İkizler burcunun M.Ö 501 yılında 31 derece 42 dakika ancak M.S 2000 yılında 7 derecelik bir farkla 24 derece 42 dakika olduğunu görürsünüz.
İkincisi ve daha da önemlisi ise çiftler arasında simetri olmaması. M.Ö 501 yılında İkizler 31 derece 42 dakikadayken onunla simetrik olması gereken Oğlak burcu 27 derece 33 dakikada. M.S 2000 yılında ise İkizler burcu 24 derece 42 dakikada iken Oğlak burcu 34 derece 4 dakikada. Bunun sebebi 30 derecelik segmentlerin doğuş zamanları arasındaki simetrinin ekinoks noktalarından birine göre değil yalnızca takımyıldızlara göre hesaplanması.
Aşağıdaki tabloyu inceleyim;
40°Kuzey enleminde Tropikal Burçların Başlangıçlarının koordinatları:
|
270°-60° Tropical Longitude Oğlak Kova Balık Koç Boğa İkizler Long. 270.00 300.00 330.00 0.00 30.00 60.00 R.A. 270.00 302.18 332.09 0.00 27.91 57.82 Decl. -23.45 -20.16 -11.48 0.00 11.48 20.16 A.D. -21.34 -17.94 -9.81 0.00 9.81 17.94 O.A. 291.35 320.13 341.90 0.00 18.10 39.88 R.T. 28.78 21.77 18.10 18.10 21.77 28.78 90°-240° Tropical Longitude Yengeç Aslan Başak Terazi Akrep Yay Long. 90.00 120.00 150.00 180.00 210.00 240.00 R.A. 90.00 122.18 152.09 180.00 207.91 237.82 Decl. 23.45 20.16 11.48 0.00 -11.48 -20.16 A.D. 21.34 17.94 9.81 0.00 -9.81 -17.94 O.A. 68.66 104.24 142.28 180.00 217.72 255.76 R.T. 35.59 38.04 37.72 37.72 38.04 35.59
|
Yukarıdaki tablodaki kısaltmalar yukarıdan aşağıya;
- kolon (Long); her burcun başlangıcının tropikal boylamını,
- kolon (R.A); her burcun başlangıcının ilk sağ açıklık derecelerini,
- kolon (Decl.); her burcun başlangıcındaki ekliptik deklinasyon derecelerini,
- kolon (A.D.); her burcun başlangıcındaki yükseklik farkını,
- kolon (O.A.); daha önce açıkladığımız eğik yükseklik derecesini
- kolon (R.T.); belirtilen boylamda burcun doğuş zamanını belirtmektedir.
Yukarıda daha önce sözünü etmediğimiz “A.D.” yani sağ açıklık farkına kısaca değinelim. Sağ açıklık derecesi farkı ya da “A.D.” basit anlatımla, bulunulan noktanın sağ açıklık derecesi “R.A.” ve yine o noktanın eğik yükseklik derecesi “O.A.” arasındaki farktır.
Öncelikle; O.A. = R.A. – A.D.
Nitekim bir noktanın sağ açıklık derecesi farkının (A.D.)bulunması için eğik yükseklik derecesinin (O.A.) bulunması gerekmektedir. Bir noktanın sağ açıklık derecesi farkı sıradaki noktanın ve o noktanın yeryüzü enleminin aşağıdaki formülle hesaplanmasından türetiliyor;
A.D. = arcsin(tan Decl. x tan Latitude)
Bu bağlantılar yukarıda paylaştığımız koordinat tablosunda görülebilir. Tablodaki 330 dereceden ya da isimlendirirsek Balık burcunun eğik yükseklik derecesinden 360 ya da 0 derecenin yani Koç burcunun eğik yükseklik derecesine olan kavis (arc) ile 0 derece ya da Koç burcunun eğik yükseklikderecesinden 30 derecenin yani Boğa burcunun eğik yükseklik derecesine doğru olan kavis (arc) aynıdır. Bu kavisler tropik Balık ve Koç burçlarının doğuş zamanlarıdır. Bu durum iki olgunun sonucudur; birincisi 0 Derece tropikal balık burcundan 0 derece tropikal Koç burcuna doğru olan kavis ile 0 derece tropikal Koç burcundan 30 derece tropikal koç burcuna (yani 0 derece Boğa burcuna) doğru olan kavisin aynı olması. İkincisi ise, 0 derece tropikal Balık burcunun deklinasyonu, 30 derece tropikal Koç burcunun deklinasyonun tam olarak zıttı olması. Geri dönüp tabloyu incelersek Balık burcunun deklinasyonunun -11.477 derece, Koç burcunun deklinasyonunun ise +11.477 olduğunu görürüz. Bu sıralama, 0 derece tropikal Balık burcunun sağ açıklık derecesi farkının (A.D.), 30 derece tropikal Koç burcunun sağ açıklık farkına (A.D.) tam olarak zıt olmasına sebep olur.
Sadece bir şartla; iki nokta, ekinoks noktalarıyla simetrik olarak ilişkilendirilirse eğik yükseklik derecesi bakımından bu simetri yakalanabilir ki bu sıralama da ekinoks noktalarından eşit uzaklıkta olan burçların simetrik doğuş zamanlarını ortaya çıkarır. Bu simetri bir Sidereal Zodyak’ta ancak Bahar Ekinoksu noktası tam olarak burcun 0 derecesinde olduğu zaman gerçekleşir ki Sistem A ve B yi tasarlayan Babillililer bunu biliyorlardı ve bu yüzden 30 derecelik segmentleri 0 derece Koç burcuna göre değil de Bahar Ekinoksu noktasına göre hesaplıyorlardı.
Buradan hareketle astroloji disiplininin yalnızca burçlardan ibaret olmadığını,ışıkların (Ay, Güneş) gezegenlerin, asteroidlerin, hatta varsayımsal noktaların birbirlerine yaptığı açıların da burçlar kadar belirleyici olduğu sonucuna varabiliriz. Bu sebeple mevsimlere dayalı olan astrolojinin geçerliliği her zaman vardı ve var olacak. Bunun değiştirilmemesinin yukarıda belirtildiği gibi bir sebebi var.
13. BURÇ SORUNSALINA DAİR
Güneş, Akrep ve Yılancı takımyıldızlarının boylamına aynı anda girer ve bu boylamda aynı zaman uzunluğunda kalır. Yılancı takımyıldızının ekliptik üzerinden geçtiği doğrudur ancak bu onu yalnızca zodyağın bir parçası yapar, yeni bir burç yapmaz. Bunun sebebi de konu Zodyak olduğu için yalnızca gökcisimsel boylamın (celestial longitude) dikkate alınmasından ileri gelir. Yılancı’nın kuyruğu, boylam olarak Akrep takımyıldızının boylamıyla aynıdır. Bu yüzden 13. Burç olarak sayılamaz. Aslında bir bütün olarak bakarsanız özellikle Hint disiplininde “Ophiuchus vel Serpantarius” olarak geçen bir eliyle yılanı kavramış, bir ayağıyla ise akrebin kuyruğuna basan şamanik bir figürdür. Aslında figürdeki yılan da binyıllar boyunca bir bütün olarak alınmış ancak Uluslararası Astronomi Birliği (IUA) binlerce yıllık geleneği bozarak yılanın başı (Serpent Caput) ve yılanın kuyruğu (Serpent Cauda) olarak ikiye ayırmıştır.
Boylam konusunda daha fazla açıklık getirmek gerekirse;
• Akrep takımyıldızının en baştaki yıldızları sırasıyla, kuzeydeki pençede konuşlanmış
Xi Scorpii yıldızı (1°18' YAY) ve kafa bölgesinde yer alan Delta Scorpii (Dschubba) (2°34' Yay)
yıldızıdır.
• Ophiuchus yani Yılancı takımyıldızının en baştaki yıldızı ise Yed Prior’dur (2°18' Yay).
Sol eliyle yılanı kavrar.
• Akrep takımyıldızının, aslında akrebin kuyruğundan itibaren karanlık gökyüzüne baktığımızda
fark edebileceğimiz Samanyolu galaksisinin o bulutumsu kısmında bulunan son yıldızları ise
sırasıyla; akrebin iğnesinin yanındaki Acumen (M7 Sccorpii) (28°43' Yay) ve iğnenin altındaki
NGC 6496 Globular yıldız kümesidir (29°48' Yay).
• Ophiuchus yani Yılancı takımyıldızının son yıldızı yılanı kavrayan sol elindeki Sinistra
(Nu Ophiuchi) yıldızıdır (29°45' Yay)
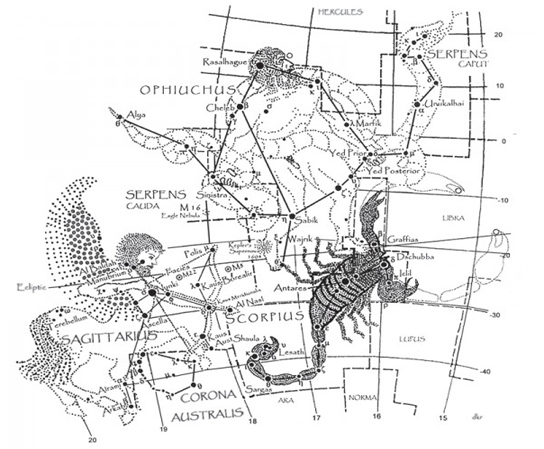
Bu durumda Yılancı takımyıldızı yalnızca dışarıda bulunan sönük yıldızları hesaba katmamız şartıyla Akrep takımyıldızından uzun olabilme şansı vardır ancak burada Zodyak’tan bahsettiğimiz için şunu kaçırmamamız gerek; dikkatli bakarsanız Zodyak çizgisi üzerinde, Yay burcunda yayı tutan figürün Ophiuchus’un dışarıdaki sönük yıldızlarının boylamından daha önce geldiğini görürsünüz. Dolayısıyla Ophiuchus yani Yılancı takımyıldızı daha uzun bir Zodyak figürü olarak değerlendirilemez. Zodyak’ta bu yüzden 13. Burç yoktur. Bu durum olsa olsa astrologların da unutmaya yüz tuttuğu Yılancı-Akrep burcu bütünlüğü olarak değerlendirilebilir.
Barış Özbayraktar
(Astroloji Akademisi İleri Seviye)
Not: Bu yazı ilk defa astrolojimarket.com adresinde 2016 yılında yayınlanmıştır.
Kaynakça;
1) Robert Hand – On the invariance of the tropical zodiac (http://arhatmedia.com/tropzo.htm)
2) Otto Neugebauer – The History of Ancient Mathematical Astronomy https://books.google.com.tr/books?id=6tkqBAAAQBAJ&lpg=PA1188&ots=EGaXkuGKOC&dq=Neugebauer%20in%20the%20History%20of%20Ancient%20Mathematical%20Astronomy&hl=tr&pg=PR1#v=onepage&q&f=false
3) Diana K. Rosenberg – Tyson’s Zodiac: Are There Really Fourteen Signs? ( http://ye-stars.com/WP/wp-content/uploads/TMA1209rosenberg.pdf )
4) Devrim Yılmazer – Tetrabiblos (Tetrapedia)
Ophiuchus (serpent bearer) : http://chandra.harvard.edu/photo/constellations/ophiuchus.html
Scorpius (The Scorpion)http://chandra.harvard.edu/photo/constellations/scorpius.html